Multitask Active Learning for Graph Anomaly Detection

文献地址：Multitask Active Learning for Graph Anomaly Detection

代码仓库：AhaChang/MITIGATE

文献介绍了一种名为 MITIGATE 的多任务主动学习框架，用于在图结构数据中进行异常检测。

介绍

背景

现有的图神经网络（GNN）在异常检测中面临的一个主要挑战是缺乏足够的标注数据，这导致模型性能不稳定。

现有问题

• 无监督方法通常依赖于数据的分布模式，但如果数据偏离假设的分布，其性能会明显下降。
• 图结构数据的复杂性以及手动标注正常节点和异常节点的高成本，限制了完全监督学习的应用。由于获取充足的标签非常昂贵，因此需要探索能够利用有限监督信号的学习范式。

MITIGATE框架

该框架通过结合节点分类任务来检测异常，主要创新点包括：

1. 多任务学习：MITIGATE 利用了节点分类任务的监督信号来帮助异常检测，特别是在没有已知异常的情况下，通过分类任务检测分布外的节点。
2. 动态信息性度量：通过不同任务之间的置信度差异来度量节点的信息性，从而选择那些提供有用信息但不会过于复杂的样本进行训练。
3. 掩码聚合机制：为了解决图结构中节点间的关系，MITIGATE 采用了一种掩码聚合机制来度量节点的代表性，考虑了节点的固有特性和已标注状态。

实验结果

MITIGATE 在四个数据集上的实验结果表明，该方法在异常检测任务中显著优于现有的最先进方法。它不仅能够更有效地利用有限的标签数据，还通过主动查询策略来选择最有代表性和信息性的节点进行标注，从而提升了模型性能。

主要贡献

• 提出了 MITIGATE 框架，通过结合外部监督信号和主动查询策略，在有限的标注预算下进行图异常检测。
• 设计了一种动态的节点选择策略，基于置信度差异和代表性来选择最有价值的节点。
• 在多个数据集上的实验验证了该方法的有效性，并且在 AUC-ROC 和 AUC-PR 等指标上显著优于其他方法。

MITIGATE 框架的关键在于如何通过多任务学习和主动学习相结合，提升图异常检测的效率，同时降低标注成本。

2. 问题定义

在本节中定义了基于主动学习的图异常检测问题。

设 $G = (V, A, X)$ 为一个属性图，其中 $V = \{v_1, v_2, \dots, v_n\}$ 是节点集合，$A \in \{0, 1\}^{n \times n}$ 为邻接矩阵，$X \in \mathbb{R}^{n \times k}$ 为节点属性矩阵。需要注意的是，在现实世界中异常标签很少，但部分分类标签是可以获取的。我们将被标注为分类任务的节点集合记为 $V_N^L$，对应的标签为 $Y_N^L \in \mathbb{R}^{n \times C}$，其中 $C$ 表示类别数。节点 $v_i$ 的分类标签为独热标签 $y_N^i$。异常检测标签记为 $Y_t^L \in \{0, 1\}$，表示第 $t$ 次迭代中节点是否为正常或异常，节点 $v_i$ 的异常检测标签为 $y_A^i$。

我们初始化一个分类标签节点的集合，即 $V_0^L = V_N^L$，并将它们视为正常节点，$Y_0^L = \{0\}$。

我们在附录 A 中总结了本文的关键符号。

给定一个属性图 $G$、一个查询策略 $Q$、一个标注预算 $B$，基于主动学习的异常检测算法的目标是在每次选择后从未标注节点集合 $V_t^U$ 中选择一个子集 $S_t$，并标注它们，以最小化模型 $M$ 的损失：

$$\min_{V_t^L} L(M, Q | G, Y_t^L, Y_N^L)$$

其中 $V_t^L = V_{t-1}^L \cup S_t$，且 $V_t^U = V_{t-1}^U \setminus S_t$，分别为第 $t$ 次选择后的已标注集合和未标注集合。$t \in \{1, 2, \dots, B/b\}$，$b$ 是每次迭代中的预算。接着，图 $G$、分类标签 $Y_N^L$ 以及异常检测标签 $y_A^i$ 将用于训练模型 $M$。为了方便起见，我们将标注预算定义为允许标注的最大节点数。

3. 方法

在本节中，我们介绍了提出的 MITIGATE 框架。首先，我们概述整个框架，然后详细说明选择策略，包括用于聚类的距离特征计算和跨任务置信度差异的计算，最后介绍 MITIGATE 的训练过程。

3.1 框架概述

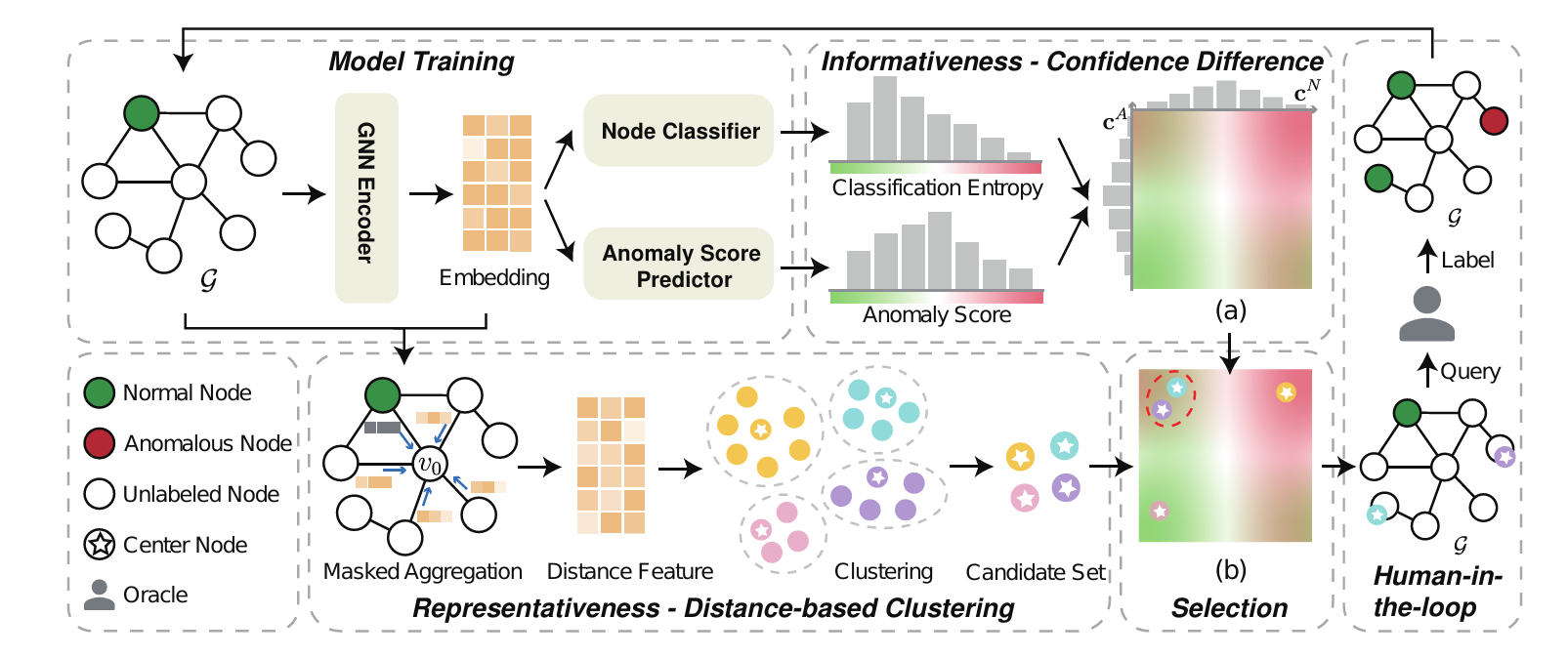
MITIGATE 的工作流程如图 1 所示。它利用一个共享的编码器来进行节点表示学习，并分别为节点分类和异常评分预测设计了两个解码器。考虑到多任务结构，我们设计了一种基于任务间置信度差异的节点信息性度量。为了减少初始的性能差距，我们将分类不确定性纳入信息性评分的计算中。为了在每一步中提升节点选择的多样性，我们采用了 K-Medoids 聚类算法，将聚类中心视为代表性样本，并引入了一种基于掩码聚合的新颖距离度量。随后，我们从这些中心中选择信息性得分最高的节点，提供给专家标注，确定它们是否为异常节点。最后，选择的节点集将加入已标注集，继续训练模型。

MITIGATE 的整体框架由以下几个核心部分组成：

• 编码器：用于学习节点的表示。
• 节点分类器：用于预测节点类别，利用分类结果的不确定性进行异常检测。
• 异常评分预测器：用于给每个节点打分，判断其是否异常。
• 混合异常评分：结合分类器和异常评分预测器的结果，生成最终的异常评分。

MITIGATE 算法流程介绍

输入参数：

• 图结构数据： $G = (V, A, X)$，其中$V$是节点集合，$A$是邻接矩阵，$X$是节点属性矩阵。
• 查询批次大小： $b$，每次迭代中需要查询的节点数量。
• 总预算： $B$，最大允许查询的节点数。
• 节点分类任务的已标注集合： $V^L_N$，已标注用于分类的节点集合。
• 聚类的簇数： $m$，K-Medoids 聚类中的簇数。

输出：

• 异常评分： $s$，算法为每个节点输出的最终异常评分。

算法步骤：

1. 初始化标注和未标注集合：

   • 将初始分类任务中的已标注节点集合设置为 $V^0_L = V^L_N$，未标注集合为 $V^0_U = V \setminus V^L_N$，即图中所有未标注的节点。

2. 开始迭代：

   • 迭代从 $t = 1$ 到 $\frac{B}{b}$，每次迭代从未标注节点集合中选择 $b$ 个节点进行标注。

3. 训练模型：

   • 使用当前标注集合 $V^{t-1}_L$ 和初始标注集合 $V^L_N$ 训练模型 $M$。

4. 计算掩码聚合距离特征：

   • 通过掩码聚合机制计算节点的距离特征 $\hat{H}$，以考虑节点的邻域信息和标注状态。

5. 计算未标注节点之间的距离：

   • 对未标注节点集合 $V^{t-1}_U$ 中的每一对节点 $v_i$ 和 $v_j$ 计算距离 $\text{dist}(v_i, v_j)$。

6. 进行 K-Medoids 聚类：

   • 对未标注节点集合 $V^{t-1}_U$ 进行 K-Medoids 聚类，生成 $m$ 个簇中心。

7. 计算置信度差异和信息性得分：

   • 使用公式 (11) 和 (12) 计算每个节点的置信度差异 $d$ 和信息性得分 $Info$。

8. 选择信息性得分最高的节点：

   • 根据信息性得分从每个簇中选择 $b$ 个信息性得分最高的簇中心组成 $S_t$，这些节点将被标注。

9. 查询专家进行标注：

   • 向专家查询 $S_t$ 中节点的标签，并标注这些节点是否为异常。

10. 更新标注和未标注集合：

    • 将新标注的节点集合 $S_t$ 加入已标注集合 $V^t_L = V^{t-1}_L \cup S_t$，从未标注集合 $V^t_U = V^{t-1}_U \setminus S_t$ 中移除这些节点。

11. 重复训练：

    • 在所有迭代完成后，使用最终标注集合 $V^B_L$ 和初始分类标注集合 $V^L_N$ 再次训练模型 $M$。

12. 计算总体异常评分：

    • 最终使用公式 (6) 计算每个节点的异常评分 $s$，结合节点分类器和异常评分预测器的结果生成最终的异常检测分数。

总结：

MITIGATE 算法通过多任务学习和主动学习相结合，逐步从未标注数据中挑选最有代表性和信息性的节点进行标注，并在每次迭代中通过分类器和异常评分预测器共同完成异常检测。在每次迭代中，使用掩码聚合特征和 K-Medoids 聚类选出代表性节点，然后依据置信度差异选择最有价值的节点进行标注，最终获得准确的异常评分。

3.1.1 编码器

编码器的目的是将图的拓扑结构和节点属性映射到潜在空间中。我们采用图卷积网络（GCN）来学习节点表示，其层级传播定义如下：

$$H^{(l+1)} = \sigma \left( D^{-\frac{1}{2}} \tilde{A} D^{-\frac{1}{2}} H^{(l)} W^{(l)} \right)$$

其中，$\tilde{A} = A + I$，$D$ 为度矩阵，$I$ 是单位矩阵，$W^{(l)}$ 是第 $l$ 层的权重矩阵，$H^{(l)}$ 为第 $l$ 层的节点表示，$\sigma$ 是激活函数。

3.1.2 节点分类器

节点分类器采用一个图卷积层，进一步保留中间节点表示的结构信息，公式如下：

$$Z = \sigma \left( D^{-\frac{1}{2}} \tilde{A} D^{-\frac{1}{2}} H W_N \right)$$

其中，$H$ 是编码器的最终输出，$W_N$ 是节点分类器的权重矩阵。由于异常节点在分类过程中往往具有较高的不确定性，我们采用熵作为异常概率的衡量标准，熵得分越高，节点越有可能为异常节点。节点分类器对节点 $v_i$ 的熵得分为：

$$e_i = -\sum_{j=1}^{C} z_{ij} \log z_{ij}$$

3.1.3 异常评分预测器

异常评分预测器基于共享的节点表示，通过线性变换和 Sigmoid 函数来生成异常评分，公式如下：

$$p = \text{Sigmoid}(W_A H + b_A)$$

其中，$p \in \mathbb{R}^n$ 为预测的异常评分，$W_A$ 为权重矩阵，$b_A$ 为偏置项。

3.1.4 混合异常评分

考虑到节点分类器和异常评分预测器都有能力检测异常节点，我们采用加权评分函数，将两个预测结果结合生成最终异常评分，公式如下：

$$s = \text{Norm}(e) + \phi \cdot \text{Norm}(p)$$

其中，$s \in \mathbb{R}^n$ 为总体异常评分，$\text{Norm}(e)$ 和 $\text{Norm}(p)$ 分别为熵得分和异常评分的标准化结果，$\phi$ 是权重超参数，用于平衡两个预测结果的重要性。

3.2 节点选择

为了提升统一框架在异常检测中的整体表现，我们根据代表性和信息性来衡量节点的价值。

3.2.1 基于距离的聚类

为了从大量未标注数据池中发现具有代表性的样本，我们设计了一种掩码聚合机制，用于生成考虑邻域特征和已标注节点状态的距离特征。传统的欧几里得距离常用于表示间的距离计算，但在图结构中，直接聚合邻域信息可能会掩盖中心节点的特征。因此，我们通过掩码聚合机制来计算距离特征，具体公式为：

$$\hat{h}_i^t = \frac{\text{SUM}(h_j, \forall v_j \in N(v_i) \cap V_U^{t-1})}{|N(v_i)|} + h_i$$

其中，$N(v_i)$ 是节点 $v_i$ 的邻居集合，$V_U^{t-1}$ 是第 $t-1$ 次选择后的未标注节点集合。节点 $v_i$ 和 $v_j$ 之间的距离计算公式为：

$$\text{dist}(v_i, v_j) = || \hat{h}_i^t - \hat{h}_j^t ||^2$$

3.2.2 置信度差异

节点分类器和异常评分预测器的置信度可以用于识别异常。节点分类器的预测熵得分越高，置信度越低，异常评分预测器的异常得分越高，置信度越高。我们使用曼哈顿距离来量化两个任务之间的置信度差异，公式如下：

$$d = |c_A - c_N|$$

其中，$c_N$ 和 $c_A$ 分别表示节点分类器和异常评分预测器的置信度。

3.2.3 节点选择

为了从未标注节点集合中选择合适的样本进行标注，我们引入了一种基于时间动态变化的节点信息性度量。初期，节点分类器为异常检测提供初始预测，随着训练的进行，我们逐渐转向关注置信度差异较大的节点。信息性得分的计算公式为：

$$Info = \tau |V_L^t| \text{Norm}(e) + (1 - \tau |V_L^t|) d$$

其中，$|V_L^t|$ 表示第 $t$ 次迭代中已标注节点的数量，$\tau$ 是衰减参数。该信息性评分首先受异常影响较大，随着训练的深入，转而关注任务之间预测冲突的节点。

3.3 模型训练

在每次查询后，MITIGATE 的训练通过优化三个方面来持续进行。首先，在预先标注的节点上，我们对节点分类进行交叉熵损失计算：

$$L_{nc} = -\frac{1}{|V_N^L|} \sum_{v_i \in V_N^L} \sum_{j=0}^{C} y_{N_i}^j \log z_i^j$$

接下来，我们在每次迭代中的标注节点上，对异常检测进行加权的二元交叉熵损失计算：

$$L_{ad} = -\frac{1}{|V_L^t|} \sum_{v_i \in V_L^t} \left( \gamma_t y_A^i \log p_i + (1 - y_A^i) \log(1 - p_i) \right)$$

其中，$\gamma_t$ 是异常节点相对于正常节点的比例。

最后，我们通过优化已标注节点集合上的分类预测不确定性，进一步提升异常检测的效果：

$$L_{un} = -\frac{1}{|V_L^N|} \sum_{v_i \in V_L^N} \sum_{k} z_{ik} \log z_{ik} + \frac{1}{|V_L^A|} \sum_{v_j \in V_L^A} \sum_{k} z_{jk} \log z_{jk}$$

综合来说，MITIGATE 的总体损失函数为：

$$L = \alpha \cdot L_{nc} + \beta \cdot L_{ad} + L_{un}$$

其中，$\alpha$ 和 $\beta$ 为损失函数的权重参数。