论文地址：Effective High-order Graph Representation Learning for Credit Card Fraud Detection

代码仓库：AI4Risk/antifraud: A repository for financial fraud detection

背景，动机，创新

1 背景

随着数字支付的普及，信用卡欺诈已成为全球金融系统中的重大问题，带来巨大的经济损失，并影响个人和企业的财务安全。报告预测未来十年全球信用卡欺诈损失将达数千亿美元，因此有效的欺诈检测技术对于维持金融系统的健康至关重要。

2 动机

image-20241112232509078

现有的欺诈检测方法，包括基于规则和传统的机器学习方法，难以识别复杂的欺诈行为，特别是那些伪装性强的间接交易。在这种情况下，欺诈者会通过多个正常用户和合法交易掩盖其身份，绕过检测系统，使得欺诈交易看起来像普通的多跳间接交易。虽然近年来图神经网络（GNN）因其在捕捉节点间关系方面的优势而被应用于欺诈检测，但现有的GNN方法在识别这种伪装交易时效果有限。主要原因在于：

  1. 伪装欺诈的复杂性：欺诈者往往利用多跳间接交易来隐藏自己，使得直接邻居大多为正常节点，违反了GNN中的同质性假设（即相似节点更可能相连）。因此，欺诈者在网络中的特征变得不明显，导致模型难以分辨正常和欺诈节点。

  2. 过度平滑问题：当GNN层数增加时，节点的特征可能会过于平滑，导致节点表示变得模糊，无法有效区分不同类别的节点。在伪装欺诈的检测中，为了捕捉多跳间接关系，模型往往需要较深的层次，但这会进一步加剧过度平滑的问题，使得高阶信息与低阶噪声混合，导致检测效果不佳。

3 创新点

  1. 高阶交易图的构建与“纯表示”学习：

    • 传统的图神经网络方法在引入高阶信息时，会将高阶信息与低阶信息混合传播到中心节点。这种方式虽然能够捕捉多跳关系，但容易引入低阶噪声，影响检测效果。
    • 本文提出了通过解耦不同阶层的邻居节点构建高阶交易图的方法。该方法确保每一阶的信息在传播时不会被低阶噪声污染，从而实现了“纯表示”的学习。通过这种方式，模型能够更有效地识别出欺诈者利用多跳间接交易隐藏身份的行为。

  2. 专家混合注意力机制：

    • 本文引入了一种专家混合注意力机制，用于自动确定不同阶层的信息在最终节点表示中的重要性。具体而言，模型将每一层的图神经网络视为一个独立的“专家网络”，通过门控网络分配不同阶层的权重。
    • 这种注意力机制能够自适应地选择最具信息量的阶层特征，提高模型的整体检测效果。相比于传统的静态加权方法，这种动态权重分配方式使得模型在应对复杂的伪装欺诈行为时更加灵活和有效。

  3. 嵌入融合以保留多跳依赖关系：

    • 尽管高阶交易图能够传递纯净的高阶信息，但它可能会丢失原始图中的多跳依赖关系。为了保留这些依赖关系，HOGRL将原始图的嵌入与高阶图的嵌入融合在一起，以形成最终的节点表示。
    • 这种融合策略不仅保留了多跳依赖关系，还增强了模型的表达能力，使其在捕捉欺诈者伪装行为的同时，保留了网络结构中的重要信息。

  4. 实验验证的显著提升：

    • HOGRL在多个数据集上的广泛实验表明，本文方法在欺诈检测性能上优于现有的基线方法，尤其是在真实的信用卡欺诈数据集和公开的欺诈检测数据集（如YelpChi和Amazon）上展示出显著的优势。
    • 模型在各种性能指标（如AUC、F1分数、GMean）上均实现了显著提升，证明了本文方法在解决伪装多跳间接交易中的有效性。

  5. 模型的鲁棒性与可解释性分析：

    • 作者还通过参数敏感性和可解释性分析进一步验证了HOGRL的有效性。通过调整参数和可视化分析，证明了HOGRL在不同层数和参数配置下的稳定性，以及其在区分欺诈和正常节点方面的优势。
    • 可解释性分析表明，高阶图能够有效增强欺诈节点的同质性，减少聚合过程中噪声的影响，使得HOGRL的检测结果更具可解释性和可靠性。

方法论

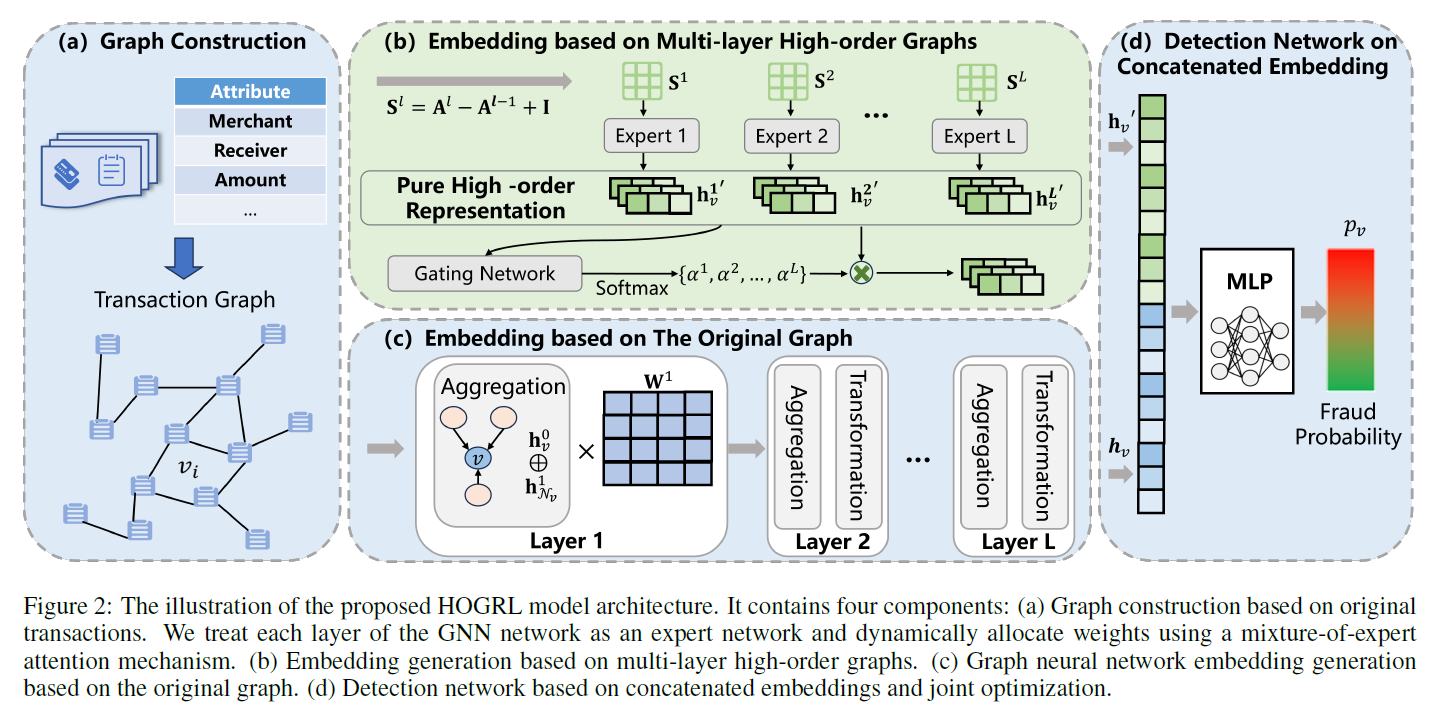
模型主要分为四个部分：交易图的构建、基于多层高阶图和原始图的节点嵌入生成、以及检测网络。

image-20241112234636718

1 预备知识

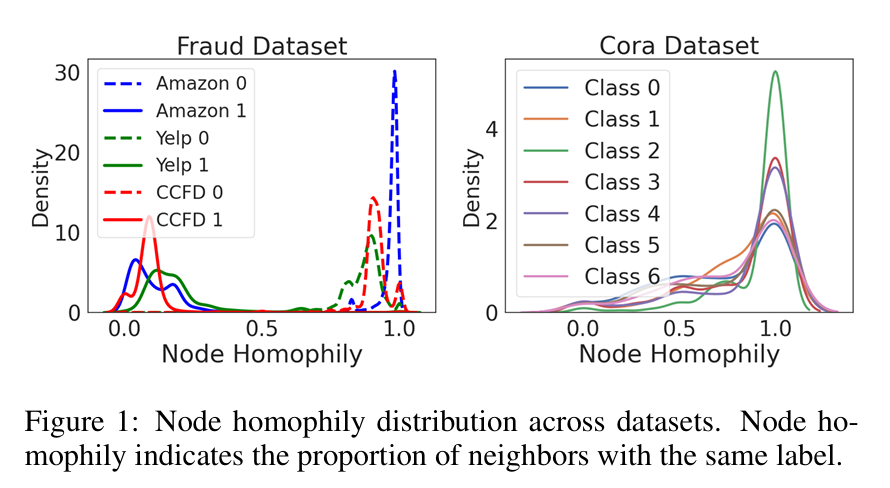
节点同质性（Node Homophily）：节点(v)的同质性表示为其邻居中与它具有相同标签的比例，公式如下：

其中和分别表示节点和节点的标签，是节点的邻居集合。这一指标在欺诈检测中尤为重要，因为欺诈节点的直接邻居可能是正常节点，从而导致低同质性。

信用卡交易图的定义：在信用卡欺诈检测中，将信用卡交易定义为图，其中表示一组交易（即节点），表示交易之间的边连接。为特征矩阵，其中每行表示节点的特征向量，为特征维度。定义为欺诈标签集合，其中（0代表正常，1代表欺诈）。的拓扑信息用邻接矩阵描述，其中表示节点和节点之间存在边。

2 高阶图的生成

GNN的基本假设是，通过特征传播和聚合利用邻居信息可以提高中心节点的预测性能。然而在伪装场景中，欺诈节点的低阶邻居通常为多个正常节点，这与GNN的假设相悖。这意味着需要引入更高阶的欺诈信息来识别伪装的欺诈者。

但是现有的高阶GNN大多依赖于混合阶传播，在引入高阶信息的同时，各阶的信息被混合并传播到中心节点，这可能会使高阶信息被低阶噪声污染。为了解决这一问题，提出了将不同阶的邻居节点解耦以构建高阶交易图的方法。

高阶交易图的阶邻接矩阵定义如下：

其中为单位矩阵。公式中的表示第阶高阶图的邻接矩阵，它包含了从中心节点出发正好能够通过跳到达的节点，从而避免了低阶邻居的干扰。

节点在第阶邻接矩阵下的邻居集合表示为：

这一集合表示节点的纯高阶邻居集合，确保了在第阶传播中只包含通过跳访问的节点，从而保持了高阶信息的纯净性。

3 图表示学习

对于第阶高阶交易图，聚合过程表示为：

其中为第阶高阶交易图的参数矩阵。由于每层高阶图对最终节点嵌入的贡献有所不同，通过引入了专家混合注意力机制，以自动确定不同层高阶图的重要性。

具体来说，将图神经网络的每一层（上面的公式）视为一个独立的专家网络，门控网络用于分配每个专家网络输出的权重。第阶高阶图的权重表示为：

其中为第个专家网络的权重向量，为偏置项。这个机制类似于传统的注意力机制，其目标是动态调整每个专家网络输出对最终输出的影响。基于多层高阶图生成的嵌入为：

这种混合专家注意力机制使模型能够自适应地选择更有信息量的阶层特征，从而提高模型的整体性能。

在原始图的嵌入生成过程中，在GNN中采用均值操作作为聚合器，其公式为：

其中，，是第层的参数矩阵，表示连接操作。将学习到的（简记为）与相加，形成最终表示：

其中，是一个超参数，用于控制基于多层高阶图生成的嵌入的权重。这样既保留了高阶信息的纯净性，又能够保持原始图中的多跳依赖关系。

进一步扩展到多关系图（例如包含多种交易类型的图）时，将每种关系的图进行独立传播，并将生成的嵌入连接起来，公式如下：

这里的表示针对关系类型生成的嵌入，表示连接操作，这样可以综合多种关系的特征，形成更丰富的节点表示。

4 检测网络和优化

在最终的节点嵌入向量生成后，HOGRL模型使用一个多层感知机（MLP）作为检测网络，来预测每个节点是否为欺诈交易。MLP的输出是节点的欺诈概率，定义如下：

为了优化这一节点分类任务，HOGRL采用了交叉熵损失函数来衡量模型的预测结果与实际标签之间的误差。交叉熵损失函数的公式为：

其中，表示节点的真实标签（0表示正常交易，1表示欺诈交易），是模型预测的欺诈概率。

在参数优化方面，HOGRL使用了Adam优化器，它是一种基于梯度的优化算法。Adam优化器在处理稀疏梯度和适应性学习率方面有较好的效果，能够帮助模型更快地收敛。具体设置如下：

  • 初始学习率设为
  • 权重衰减系数设为

通过Adam优化器，模型能够在训练过程中逐渐减少损失函数值，从而提高预测准确性。

5 复杂度分析

相比于传统的图卷积网络（GCN），HOGRL的额外计算开销主要来源于基于高阶交易图生成节点的中间表示。具体来说，对于第阶的高阶交易图，在生成嵌入时需要进行矩阵运算：

其中，是第阶高阶图的邻接矩阵，是节点特征矩阵。为了避免直接计算（第阶邻接矩阵的幂次运算），通过右乘的方式逐步计算，公式如下：

具体的计算步骤可以写成逐步计算的形式：

其中是邻接矩阵的初始形式。通过这种方法可以有效降低计算复杂度。

在实际应用中，如果将存储为具有 个非零条目的稀疏矩阵，那么生成第 阶高阶图的嵌入所需的计算时间复杂度为 ，其中 是节点特征的维度。假设 和 都比 小得多，则总的时间复杂度为 ，与传统的GCN的计算复杂度相当。因此HOGRL模型的复杂度在处理高阶图信息时得到了优化，使其在实际应用中更为高效。